Mathematicians have not yet succeeded in finding a formula for the number of different ways a road map can be folded, given n creases in the paper. Some notion of the complexity of this question can be gained from the following puzzle invented by the British puzzle expert Henry Ernest Dudeney.
Divide a rectangular sheet of paper into eight squares and number them on one side only, as shown at top left in the illustration below. There are 40 different ways that this “map” can be folded along the ruled lines to form a square packet which has the “1” square face up on top and all other squares beneath. The problem is to fold this sheet so that the squares are in serial order from 1 to 8, with the 1 face up on top.
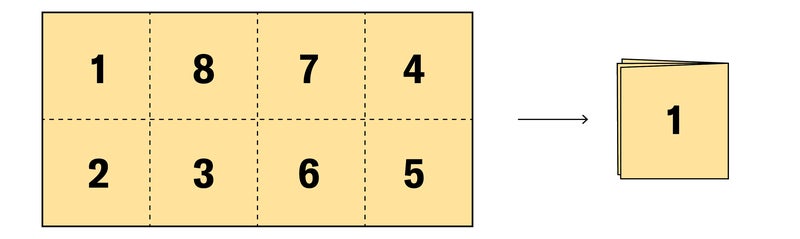
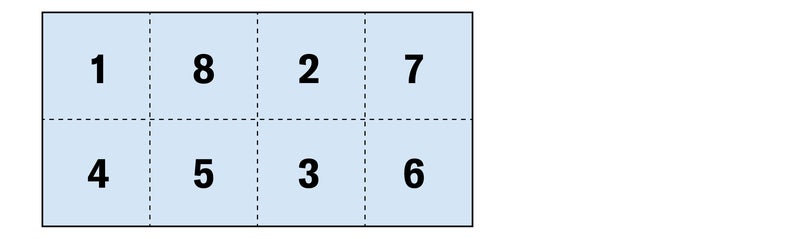
If you succeed in doing this, try the much more difficult task of doing the same thing with the sheet numbered in the manner below.
The first sheet is folded as follows. Flip the sheet over so that when you look down on it, the numbered squares are face down in this position:
Fold the right half on the left so that 5 goes on 2, 6 on 3, 4 on 1 and 7 on 8. Fold the bottom half up so that 4 goes on 5 and 7 on 6. Now tuck 4 and 5 between 6 and 3, and fold 1 and 2 under the packet.
The second sheet is first folded in half the long way, the numbers outside, and held so that 4536 is uppermost.

Fold 4 on 5. The right end of the strip (squares 6 and 7) is pushed between 1 and 4, then bent around the folded edge of 4 so that 6 and 7 go between 8 and 5, and 3 and 2 go between 1 and 4.
We’d love to hear from you! E-mail us at games@sciam.com to share your experience.
A version of this puzzle originally appeared in the May 1959 issue of Scientific American.